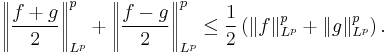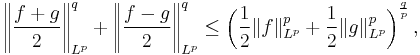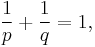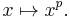Clarkson's inequalities
In mathematics, Clarkson's inequalities are results in the theory of Lp spaces. They give bounds for the Lp-norms of the sum and difference of two measurable functions in Lp in terms of the Lp-norms of those functions individually.
Statement of the inequalities
Let (X, Σ, μ) be a measure space; let f, g : X → R be measurable functions in Lp. Then, for 2 ≤ p < +∞,
For 1 < p < 2,
where
i.e., q = p ⁄ (p − 1).
The case p ≥ 2 is somewhat easier to prove, being a simple application of the triangle inequality and the convexity of